Conditional Gaussian Bayesian Networks Structure Learning

Ziwei Huang

10/06/2025

Introduction

A Conditional Gaussian Bayesian Network (CGBN) is a probabilistic graphical model that integrates discrete and continuous variables within a unified Bayesian framework, making it particularly suitable for mixed-type data. CGBNs are represented as directed acyclic graphs (DAGs), where nodes correspond to random variables and directed edges encode conditional dependencies consistent with a joint probability distribution in which continuous variables follow Gaussian distributions conditional on their discrete parents.

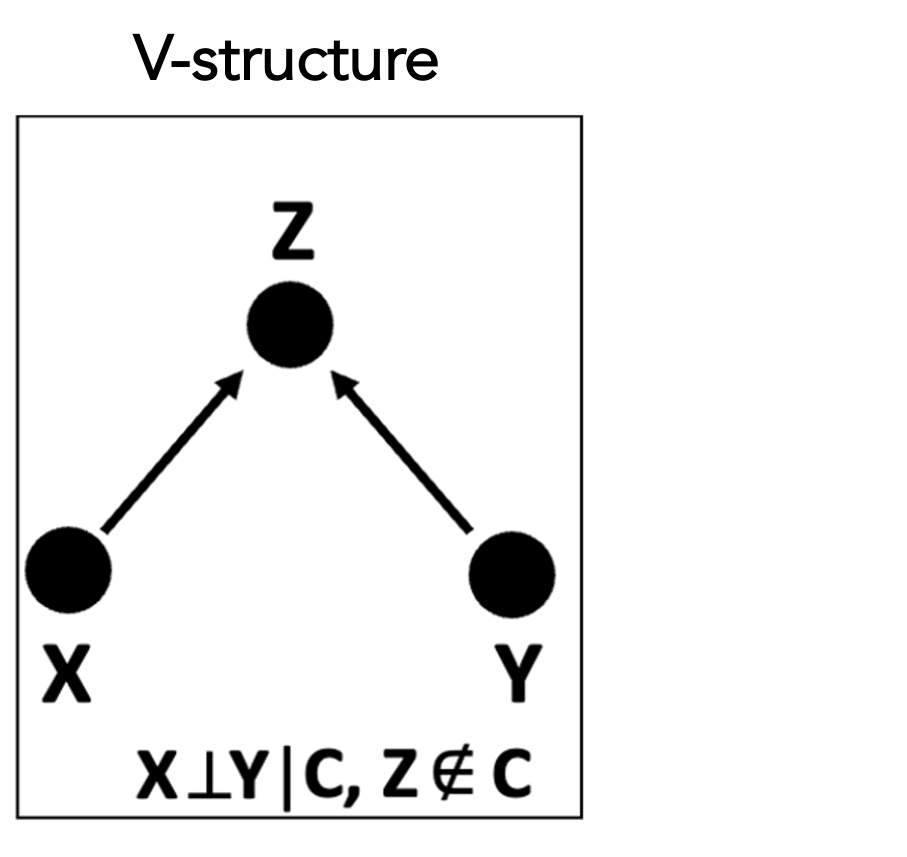
Structure learning in CGBNs is typically performed using constraint-based methods, which infer the network topology by testing conditional independence relationships implied by the data. Starting from a complete graph, edges are iteratively removed when conditional independence between variable pairs is detected given appropriate conditioning sets. A key step in orienting edges in the resulting partially directed graph is the identification of v-structures, of the form $X \rightarrow Z \leftarrow Y$. A v-structure is inferred when two variables $X$ and $Y$ are marginally independent but become conditionally dependent upon conditioning on a third variable $Z$, as illustrated in the following figure:

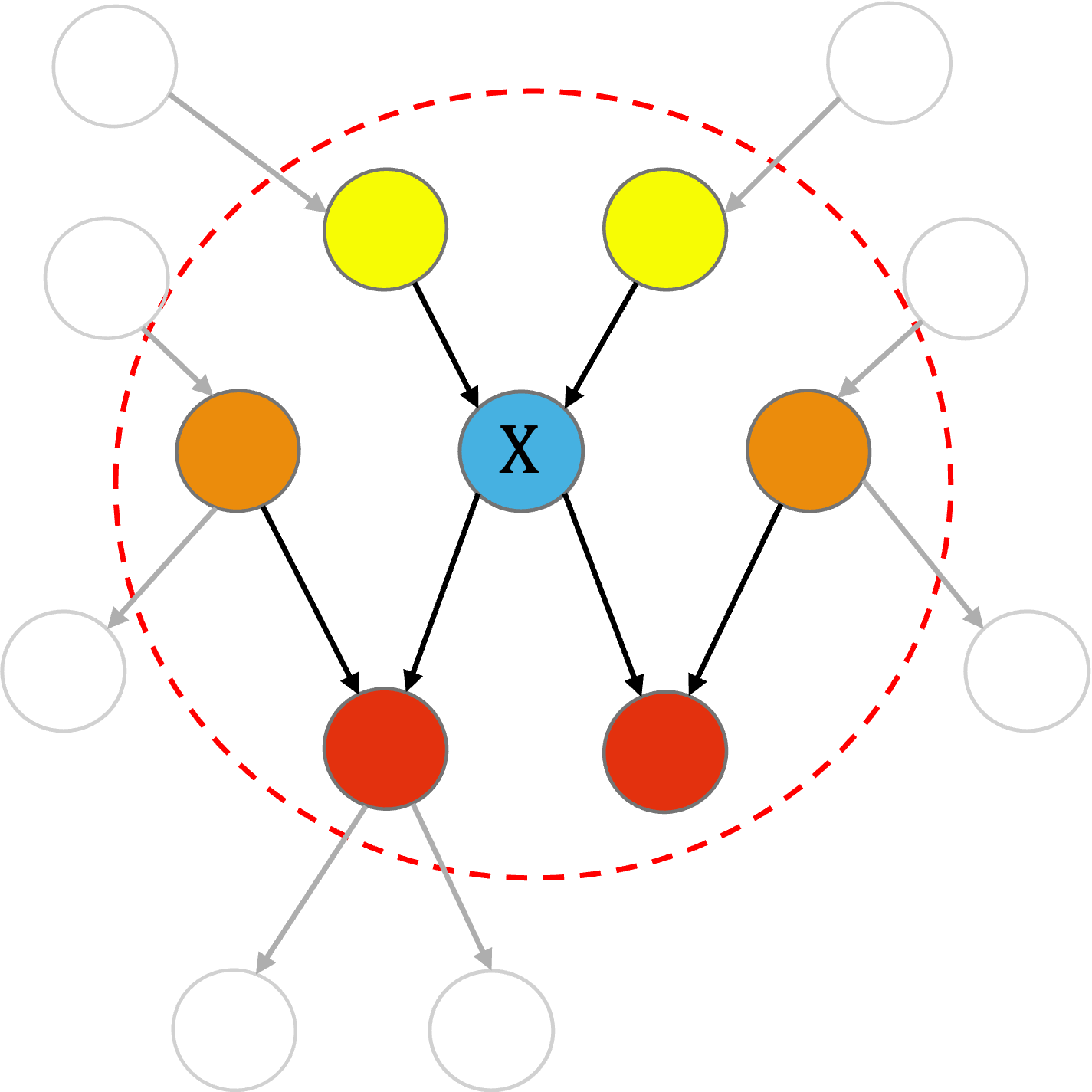
An important concept in CGBNs is the Markov blanket of a node, defined as the minimal set of variables that renders the node conditionally independent of all other variables in the network. For a given node, its Markov blanket consists of its parents, its children, and its spouses (i.e., the other parents of its children). As illustrated in the following figure, we use yellow, orange, and red to denote the parents, spouses, and children of node $X$, respectively.

RSNet implements a resampling-based structure learning framework for CGBNs, supporting four resampling strategies to improve the stability and robustness of inferred network structures:

1. Bootstrap.
2. Sub-sampling
3. Stratified bootstrap.
4. Stratified sub-sampling.

IMPORTANT NOTE: The Conditional Gaussian Bayesian Network functionalities ensemble_cgbn() and consensus_net_cgbn() are optional in RSNet and require the RHugin package. Installation instructions for macOS, windows, and Linux.

Load packages

library(RSNet)

Load a toy dataset

To illustrate the workflow, we use a synthetic toy dataset containing 20 continuous and 5 discrete variables, representing a mixed-type dataset suitable for conditional Gaussian Bayesian network analysis.

data("toy_cgbn")

Run and learn an ensemble of networks from resampled datasets

In this example, we use the simulated dataset as input and perform bootstrap resampling (boot = TRUE) with 5 iterations (num_iteration = 5). The column names of the discrete variables must be specified as a character vector in the discrete_variable argument.

To perform subsampling instead of bootstrapping, set boot = FALSE and specify the sampling proportion using the sub_ratio argument (a value between 0 and 1).

The function ensemble_cgbn() also supports parallel computing.

ensemble_toy <- ensemble_cgbn(dat = toy_cgbn, # A n x p dataframe
                              discrete_variable = sprintf("D%d",1:5), # Column names of the discrete variables
                              num_iteration = 5, # Number of resampling iteration
                              sample_class = NULL, # Optional: for stratified sampling
                              boot = TRUE, # If FALSE, perform sub-sampling
                              sub_ratio = 1, # Subsampling ratio (0–1)
                              n_cores = 1) # Number of cores for parallel computing

Consensus network construction

The construction of the consensus network for conditional Gaussian Bayesian networks (CGBNs) supports two complementary approaches:

1. method = "all": Computes the selection frequency of each edge (i.e., the proportion of resampling iterations in which the edge is identified) with respect to a reference network (typically inferred using all samples). The resulting consensus network retains its directed structure.

2. method = "average": Computes the selection frequency of each edge based on Markov blanket relationships between the two incident nodes. The resulting consensus network is undirected, representing stable dependency patterns rather than directionality.

## Directed consensus network (method = "all")
## A simple way to generate a reference network is to set: num_iteration = 1, boot = FALSE, sub_ratio = 1
reference_network <- ensemble_cgbn(dat = toy_cgbn, 
                                   discrete_variable = sprintf("D%d",1:5), 
                                   num_iteration = 1, 
                                   sample_class = NULL, 
                                   boot = FALSE, 
                                   sub_ratio = 1, 
                                   n_cores = 1)

directed_cons_net <- consensus_net_cgbn(ensemble_toy$ig_networks, # A list of igraph objects
                                        reference_network = reference_network$ig_networks$iter_1, # An igraph object
                                        method="all", # Integration method
                                        cut = 0.5) # Edge weight threshold


## Markov blanket-based undirected consensus network, set `method="average" 
undirected_cons_net <- consensus_net_cgbn(ensemble_toy$ig_networks, # A list of igraph objects
                                          reference_network = NULL, # Not required for method = "average"
                                          method="average", # Integration method
                                          cut = 0.5) # Edge weight threshold